Calculus

• tags: #Math
• Resources
  • Intro to calculus for physics
  • Highlights of calculus Prof Gilbert strang MIT watch learning Planner
• In simple terms calculus deals with things that change, like differentiation and Integration.
• Differentiation
  • Differentiation is the rate of change of a property, ie. Dividing a difference in a property by a difference in an another property. It is often known as the slope of the curve.
  • In a varying derivative like in acceleration, the smaller the change that is measured, the greater the chance for errors in measurement.
  • 
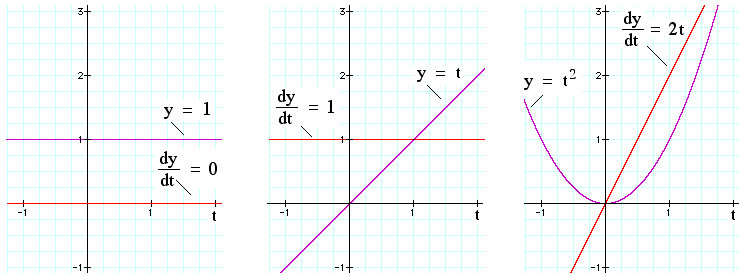
  • Sum of terms If x is increasing with rate (dx/dt) and y is increasing with rate (dy/dt), what is the rate of increase in (x+y)? if, over a certain time t+ Δt, x increases by Δx and y increases by Δy, then the change in (x+y) is (Δx+Δy).

The rate of change in the function is equal to the sum of the individual rate of changes, The derivative of the sum is the sum of derivatives - Trignometric functions - 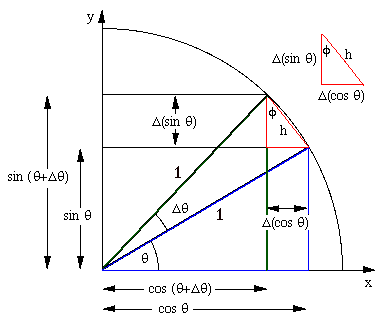- consider a circle with unit radius and we take sine as the opposite side by the hypotenuse and the Cosine as the adjacent side by the hypotenuse. For small change in the angle, Δ(sin θ) is the amount that in θ increases when θ increases by Δθ). So it must be (sin(θ+Δθ) − sin θ).

look at the small right triangle in red. We call its hypotenuse h. Applying the definition of sine and cos, and remembering that the cos θ is decreasing, we have

Δ(sin θ)  =  h cos φ      and      Δ(cos θ)  =   − h sin φ.

as Δθ becomes very small. The hypotenuse approaches more and more closely the length of the arc of the circle between the two radii. From the definition* of angle (angle in radians ≡ arc/radius) and the fact that radius is one, this arc has a length Δθ. It follows that, as Δθ becomes very small, h becomes approximately Δθ. Further, h becomes closer and closer to being at a right angle to the radius. Further, the angle φ becomes closer and closer to being equal to θ.

So, in this limit, and using the results of the previous paragraph (θ  =  φ and h  =  dθ for small enough values of Δθ), the equations above become

d(sin θ)   =   dθ cos θ     and     d(cos θ)  =   − dθ sin θ - 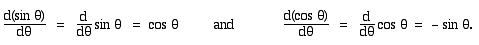- - 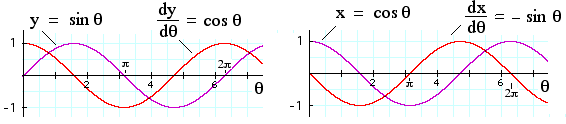The chain rule - Suppose we have a function z that depends on t, in a way that allows us to calculate z if we know t. And suppose that x depends on z in a similarly explicit way. Just by canceling a factor, we can write: -

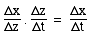
• Integration
  • 
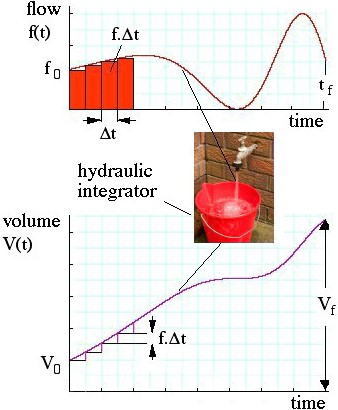
  • A bucket integrates the flow of water from a tap above it. The bucket already has in it a volume V0 of water and that we put the bucket under the tap (we start integrating) at time t  =  0. The tap is already on, with a flow rate f0, called the initial flow rate. Consider the first short interval Δt. The flow rate is by definition the volume per second so, in the first time Δt, a volume of approximately f0.Δt pours into the bucket. f0.Δt is shown by the first red rectangle on the top graph. “Approximately” is there because, during Δt, the flow is not constant, but varying.

Vf   =   V0 + f0.dt + f1.dt + f2.dt + etc until we get to tf. - 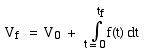- V0 is a constant of integration. Integration doesn’t tell you the complete answer, it only tells you how much something has changed during the process. You will need to find the constant of integration – very often by using the initial conditions, - Note: important practical point: when we made Δt small in differentiation, the ratio Δx/Δt became sensitive to experimental or computational error as Δt became small. This problem does not arise in multiplication. Even better, the computation errors, being sometimes positive and sometimes negative, tend to cancel out. So numerical integration is much easier and safer than numerical differentiation. - The integral of t^m is (t^(m+1))/(m+1) - List of integrals

• Logarithm function
  • logarithms to base 10, 2 is the log of 100, and 3 is the log of 1000. If we multiply ten by itself only once, we get 10, so 1 is the log of 10.
  • The definition of the logarithm of a number a (to base 10) is this:
    • 10^(log a)  =  a.
  • In other words, the log of the number a is the power to which you must raise 10 to get the number a.
• The Exponential funciton
  • The number e  =  2.718… has the property that the derivative of __e__x is just __e__x.
  • The function e x is chosen and the value of e defined so that the derivative of e __x is __e __x. In other words, __e x is a curve whose slope equals its value at all points. So it is also its own integral.
  • The derivative of e ax is a.e ax, where a is a constant, and
  • The integral of e ax is e ax/a.
• Calculus